2.9 递归对象
对象可以以其他的对象作为自己的属性值。当这个类下的对象实例有一个属性的值还属于这个类时,这个对象就是一个递归对象。
2.9.1 类:链表
在之前的章节中我们已经提到过,链表 (Linked List) 由两个部分组成:第一个元素和链表剩下的部分。而剩下的这部分链表它本身就是个链表,这就是链表的递归定义法。其中,一个比较特殊的情况是空链表——他没有第一个元素和剩下的部分。
链表是一种序列 (sequence):它具有有限的长度并且支持通过索引选择元素。
现在我们可以实现具有相同行为的类。在现在这个版本中,我们将使用专用方法名来定义它的行为,专用方法允许我们的类可以使用 Python 内置的 len 函数和元素选择操作符(方括号或 operator.getitem )。这些内置函数将调用类的专用方法:长度由 __len__ 计算,元素选择由 __getitem__ 计算。空链表由一个长度为 0 且没有元素的空元组表示。
>>> class Link:
"""一个链表"""
empty = ()
def __init__(self, first, rest=()):
assert rest == Link.empty or isinstance(rest, Link)
self.first = first
self.rest = rest
def __getitem__(self, i):
if i == 0:
return self.first
else:
return self.rest[i-1]
def __len__(self):
return 1 + len(self.rest)
>>> s = Link(3, Link(4, Link(5)))
>>> len(s)
3
>>> s[1]
4以上的 __len__ 和 __getitem__ 的定义都是递归的。Python 的内置函数 len 在它接收属于用户定义的类的实例时调用了 __len__ 方法。类似地,元素选择操作符则会调用 __getitem__ 方法。因此,这两个方法定义的主体中都会间接的调用他们自己。对于 __len__ 来说,基线条件 (base case) 就是当 self.rest 计算得到一个空元组,也就是 Link.empty 时,此时长度为 0。
内置的 isinstance 函数返回第一个参数的类型是否属于或者继承自第二个参数。isinstance(rest, Link) 在 rest 是 Link 的实例或 Link 的子类的实例时为 True。
我们对于链表的类定义已经很完备了,但是现在我们还无法直观地看到 Link 的实例。为了方便之后的调试工作,我们再定义一个函数去将一个 Link 实例转换为一个字符串表达式。
>>> def link_expression(s):
"""返回一个可以计算得到 s 的字符串表达式。"""
if s.rest is Link.empty:
rest = ''
else:
rest = ', ' + link_expression(s.rest)
return 'Link({0}{1})'.format(s.first, rest)
>>> link_expression(s)
'Link(3, Link(4, Link(5)))'用这个方法去展示一个链表实在是太方便了,以至于我想在任何需要展示一个 Link 的实例的时候都用上它。为了达到这个美好愿景,我们可以将函数 link_expression 作为专用方法 __repr__ 的值。Python 在展示一个用户定义的类的实例时,会调用它们的 __repr__ 方法。
>>> Link.__repr__ = link_expression
>>> s
Link(3, Link(4, Link(5)))Link 类具有闭包性质 (closure property)。就像列表的元素可以是列表一样,一个 Link 实例的第一个元素也可以是一个 Link 实例。
>>> s_first = Link(s, Link(6))
>>> s_first
Link(Link(3, Link(4, Link(5))), Link(6))链表 s_first 只有两个元素,但它的第一个元素是一个有着三个元素的链表。
>>> len(s_first)
2
>>> len(s_first[0])
3
>>> s_first[0][2]
5递归函数特别适合操作链表。比如,递归函数 extend_link 建立了一个新的链表,这个新链表是由链表 s 和其后边跟着的链表 t 组成的。将这个函数作为 Link 类的方法 __add__ 就可以仿真内置列表的加法运算。
>>> def extend_link(s, t):
if s is Link.empty:
return t
else:
return Link(s.first, extend_link(s.rest, t))
>>> extend_link(s, s)
Link(3, Link(4, Link(5, Link(3, Link(4, Link(5))))))
>>> Link.__add__ = extend_link
>>> s + s
Link(3, Link(4, Link(5, Link(3, Link(4, Link(5))))))想要实现列表推导式 (List Comprehensions),也就是从一个链表生成另一个链表,我们需要两个高阶函数:map_link 和 filter_link。其中 map_link 将函数 f 应用到链表 s 的每个元素,并将结果构造成一个新的链表。
>>> def map_link(f, s):
if s is Link.empty:
return s
else:
return Link(f(s.first), map_link(f, s.rest))
>>> map_link(square, s)
Link(9, Link(16, Link(25)))函数 filter_link 返回了一个链表,这个链表过滤掉了原链表 s 中使函数 f 不返回真的元素,留下了其余的元素。通过组合使用 map_link 和 filter_link,我们可以达到和列表推导式相同的逻辑过程和结果。
>>> def filter_link(f, s):
if s is Link.empty:
return s
else:
filtered = filter_link(f, s.rest)
if f(s.first):
return Link(s.first, filtered)
else:
return filtered
>>> odd = lambda x: x % 2 == 1
>>> map_link(square, filter_link(odd, s))
Link(9, Link(25))
>>> [square(x) for x in [3, 4, 5] if odd(x)]
[9, 25]函数 join_link 递归的构造了一个 包含着所有在链表里的元素,并且这些元素被字符串 separator 分开 的字符串。这个结果相较于 link_expression 来说就更加简练。
>>> def join_link(s, separator):
if s is Link.empty:
return ""
elif s.rest is Link.empty:
return str(s.first)
else:
return str(s.first) + separator + join_link(s.rest, separator)
>>> join_link(s, ", ")
'3, 4, 5'递归构造 (Recursive Construction). 当以增量方式构造序列时,链表特别有用,这种情况在递归计算中经常出现
第一章我们介绍过的函数 count_partitions 通过树递归计算了使用大小最大为 m 的数对整数 n 进行分区的方法的个数。通过序列,我们还可以使用类似的过程显式枚举这些分区。
与计数方法个数的方法相同,我们利用相同的递归统计方法:将一个数 n 在最大数限制为 m 下分区包含两种情况:
- 用
m及以内的整数划分n-m - 用
m-1及以内的整数划分n
对于基线情况,我们知道 0 只有一个分区方法,而划分一个负整数或使用小于 1 的数划分是不可能的。
>>> def partitions(n, m):
"""Return a linked list of partitions of n using parts of up to m.
Each partition is represented as a linked list.
"""
if n == 0:
return Link(Link.empty) # A list containing the empty partition
elif n < 0 or m == 0:
return Link.empty
else:
using_m = partitions(n-m, m)
with_m = map_link(lambda s: Link(m, s), using_m)
without_m = partitions(n, m-1)
return with_m + without_m在递归情况下,我们构造两个分区子列表。第一个使用 m,因此我们将 m 添加到 using_m 的结果的每个元素中以形成 with_m。
分区的结果是高度嵌套的:是一个链表的链表。使用带有适当分隔符的 join_link,我们可以以易读的方式显示各个分区。
>>> def print_partitions(n, m):
lists = partitions(n, m)
strings = map_link(lambda s: join_link(s, " + "), lists)
print(join_link(strings, "\n"))
>>> print_partitions(6, 4)
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 12.9.2 类:树
树也可以用用户定义的类的实例来表示,而不是内置序列类型的嵌套实例。树是具有 作为属性的分支序列 的任何数据结构,同时,这些分支序列也是树。
内部值。 以前,我们定义树的方式是假设所有的值都出现在叶子上(参见 1.2.5)。然而在每个子树的根处定义具有内部值的树也很常见。内部值在树中称为 label。下面的 Tree 类就表示这样的树,其中每棵树都有一系列分支,这些分支也是树。
>>> class Tree:
def __init__(self, label, branches=()):
self.label = label
for branch in branches:
assert isinstance(branch, Tree)
self.branches = branches
def __repr__(self):
if self.branches:
return 'Tree({0}, {1})'.format(self.label, repr(self.branches))
else:
return 'Tree({0})'.format(repr(self.label))
def is_leaf(self):
return not self.branches例如,Tree 类可以表示 用于计算斐波那契数的函数 fib 的递归表达式树 中计算的值。下面的函数 fib_tree(n) 返回一个 Tree 的实例,该实例以第 n 个斐波那契数作为其 label,并在其分支中跟踪所有先前计算的斐波那契数。
>>> def fib_tree(n):
if n == 1:
return Tree(0)
elif n == 2:
return Tree(1)
else:
left = fib_tree(n-2)
right = fib_tree(n-1)
return Tree(left.label + right.label, (left, right))
>>> fib_tree(5)
Tree(3, (Tree(1, (Tree(0), Tree(1))), Tree(2, (Tree(1), Tree(1, (Tree(0), Tree(1)))))))并且,Tree 类的实例也可以用递归函数进行处理。例如,我们可以对树的 label 求和。
>>> def sum_labels(t):
"""对树的 label 求和,可能得到 None。"""
return t.label + sum([sum_labels(b) for b in t.branches])
>>> sum_labels(fib_tree(5))
10我们也可以用 memo 去构造一个斐波那契树。有了它,重复的子树只会被记忆版本的 fib_tree 创建一次,然后在不同大小的树中被用作分支很多次。(译者:更多关于 memo 的内容可以看 PythonDecoratorLibrary - Python Wiki 或者自行 Google 搜索)
>>> fib_tree = memo(fib_tree)
>>> big_fib_tree = fib_tree(35)
>>> big_fib_tree.label
5702887
>>> big_fib_tree.branches[0] is big_fib_tree.branches[1].branches[1]
True
>>> sum_labels = memo(sum_labels)
>>> sum_labels(big_fib_tree)
142587180在这种情况下,通过记忆节省的计算时间和内存量是相当可观的。我们现在只创建 35 个实例,而不是创建 18,454,929 个不同的 Tree 实例。
2.9.3 集合
除了列表、元组、字典,Python 还有第四种内置的容器类型:集合(set),集合字面量遵循了它的数学表示法:用大括号括起来元素们。重复的元素会在创建集合时被移除。集合是无序的,这表明元素被打印的顺序可能和他们在字面量中的顺序不同。
>>> s = {3, 2, 1, 4, 4}
>>> s
{1, 2, 3, 4}Python 的集合支持多种操作:包括成员测试、长度计算以及并集和交集的标准集合操作。
>>> 3 in s
True
>>> len(s)
4
>>> s.union({1, 5})
{1, 2, 3, 4, 5}
>>> s.intersection({6, 5, 4, 3})
{3, 4}除了 union 和 intersection 外,Python 还支持一些其他的集合方法:isdisjoint, issubset, 和 issuperset 提供了集合之间的比较。集合是可变的,可以用 add, remove, discard 和 pop 方法来一次改变一个元素。其他的一些方法提供了一次改变多个元素的功能,比如 clear 和 update。Python 的官方文档 documentation for sets 在课应该足够容易理解,并为课程填写了更多细节。
实现集合。 抽象地说,集合 (set) 是支持成员检验、并集、交集和合集的不同对象的集合 (collection)。支持将元素和集合连接在一起将返回一个新集合,该集合包含原集合的所有元素以及新元素 (如果新元素是不同的)。并集和交集返回分别出现在其中一个集合或同时出现在两个集合中的元素集合。与任何数据抽象一样,我们可以自由地在提供此 行为集合 (collection) 的集合的任何表示上实现任何函数。
在本节的其余部分中,我们将考虑实现集合的三种不同方法,它们的表示方式各不相同。我们将通过分析集合运算的增长顺序来表征这些不同表示的效率。我们将使用本节前面的 Link 和 Tree 类,它们可以为基本集合操作提供简单而优雅的递归解决方案。
作为无序序列的集合。 表示集合的一种方法是将其表示为一个元素出现次数不超过一次的序列。空集合由空序列表示。成员测试将会递归地遍历列表。
>>> def empty(s):
return s is Link.empty
>>> def set_contains(s, v):
"""当且仅当 set s 包含 v 时返回 True。"""
if empty(s):
return False
elif s.first == v:
return True
else:
return set_contains(s.rest, v)
>>> s = Link(4, Link(1, Link(5)))
>>> set_contains(s, 2)
False
>>> set_contains(s, 5)
Trueset_contains 的实现需要的时间复杂度是
>>> def adjoin_set(s, v):
"""返回一个包含 s 的所有元素和元素 v 的所有元素的集合。"""
if set_contains(s, v):
return s
else:
return Link(v, s)
>>> t = adjoin_set(s, 2)
>>> t
Link(2, Link(4, Link(1, Link(5))))在设计时,我们应该考虑的问题之一是 效率。相交两个集合 set1 和 set2 也需要进行成员测试,但这次必须测试 set1 的每个元素在 set2 中的隶属性:这会从而导致步骤数的二次增长,即为
>>> def intersect_set(set1, set2):
"""返回一个集合,包含 set1 和 set2 中的公共元素。"""
return keep_if_link(set1, lambda v: set_contains(set2, v))
>>> intersect_set(t, apply_to_all_link(s, square))
Link(4, Link(1))在计算两个集合的并集时,我们必须小心不要重复包含任何元素。该 union_set 函数还需要线性的时间来进行成员资格测试,从而导致整个过程的时间复杂的为
>>> def union_set(set1, set2):
"""返回一个集合,包含 set1 和 set2 中的所有元素。"""
set1_not_set2 = keep_if_link(set1, lambda v: not set_contains(set2, v))
return extend_link(set1_not_set2, set2)
>>> union_set(t, s)
Link(2, Link(4, Link(1, Link(5))))作为有序序列的集合。 加快集合操作的一种方法是改变表示方法,使集合元素按递增顺序排列。要做到这一点,我们需要一些方法来比较两个对象,这样我们就可以知道哪个更大。在 Python 中,可以使用 < 和 > 操作符比较许多不同类型的对象,但在本例中我们将集中讨论数字。我们将通过按递增顺序列出其元素来表示一组数字。
排序的一个优点体现在 set_contains 中:在检查对象是否存在时,我们不再需要遍历整个集合。如果到达的集合元素比要查找的元素大,则知道该元素不在集合中:
>>> def set_contains(s, v):
if empty(s) or s.first > v:
return False
elif s.first == v:
return True
else:
return set_contains(s.rest, v)
>>> u = Link(1, Link(4, Link(5)))
>>> set_contains(u, 0)
False
>>> set_contains(u, 4)
True这样可以节省多少步骤?在最坏的情况下,我们正在寻找的元素可能是集合中最大的一个,因此步骤数与无序表示相同。另一方面,如果我们搜索许多不同大小的项,我们可以预期,有时我们可以在列表开始附近的某个点停止搜索,而其他时候我们仍然需要检查列表的大部分。平均而言,我们预计需要检查集合中大约一半的项目。因此,所需的平均步数约为
通过重新实现 intersect_set,我们可以获得显著的加速。在无序表示中,此操作需要 set1 的每个元素执行了是否在 set2 的完整扫描。但是对于有序表示,我们可以使用更聪明的方法:同时遍历两个集合,跟踪 set1 中的元素 e1 和 set2 中的元素 e2。当 e1 和 e2 相等时,我们将该元素包含在交集中。
对于此算法我们做以下思考:假设 e1 < e2。由于 e2 小于 set2 的剩余元素,我们可以立即得出结论:e1 不可能出现在 set2 的剩余元素中,因此不在交集中。因此,我们不再需要考虑 e1。我们丢弃它并继续处理 set1 的下一个元素。当 e2 < e1 时,类似的逻辑查询 set2 的下一个元素。函数如下:
>>> def intersect_set(set1, set2):
if empty(set1) or empty(set2):
return Link.empty
else:
e1, e2 = set1.first, set2.first
if e1 == e2:
return Link(e1, intersect_set(set1.rest, set2.rest))
elif e1 < e2:
return intersect_set(set1.rest, set2)
elif e2 < e1:
return intersect_set(set1, set2.rest)
>>> intersect_set(s, s.rest)
Link(4, Link(5))为了估计这个过程所需的步骤数,我们观察到在每一步中我们至少缩小一个集合的大小。因此,所需的步数最多是 set1 和 set2 的大小之和,而不是像无序表示那样是大小的乘积。这是
对于用有序序列表示的集合,也可以在线性时间内计算并集,添加元素等。这些实现将作为练习留下。
作为二叉搜索树的集合。
我们可以通过将集合元素以 恰好有两个分支的树的形式 排列来做得比有序序列更好。
- 树的根的
entry保存集合的一个元素。 - 左分支中的条目包括所有小于根节点的元素。
- 右分支中的条目包括所有大于根节点的元素。
下图显示了代表集合 {1,3,5,7,9,11} 的一些树。同一个集合可以用树以许多不同的方式表示。在所有的二叉搜索树中,左分支中的所有元素都小于根节点,而右子树中的所有元素都大于根节点。
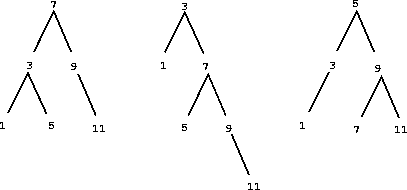
二叉搜索树表示的优点是:假设我们想要检查一个值 v 是否包含在一个集合中。我们先比较 v 和 entry。如果 v < entry,我们知道我们只需要搜索左子树;如果 v > entry,我们只需要搜索右子树。现在,如果树是“平衡的”,即每个子树的大小将是原始树的一半左右。这样,我们一步就把搜索大小为 set_contains 函数利用了树结构的集合的特点:
>>> def set_contains(s, v):
if s is None:
return False
elif s.entry == v:
return True
elif s.entry < v:
return set_contains(s.right, v)
elif s.entry > v:
return set_contains(s.left, v)将元素加入到集合的实现与搜索类似,也需要 v 与 entry 进行比较,以确定 v 应该加到右分支还是左分支,并将 v 邻接到适当的分支后,将这个新构造的分支与原始 entry 和另一个分支拼接在一起。如果 v 等于这个元素,我们就返回这个节点。如果我们被要求将 v 与一棵空树相连,我们生成一棵树,它的 entry 是 v,左右分支都是空的。函数如下:
>>> def adjoin_set(s, v):
if s is None:
return Tree(v)
elif s.entry == v:
return s
elif s.entry < v:
return Tree(s.entry, s.left, adjoin_set(s.right, v))
elif s.entry > v:
return Tree(s.entry, adjoin_set(s.left, v), s.right)
>>> adjoin_set(adjoin_set(adjoin_set(None, 2), 3), 1)
Tree(2, Tree(1), Tree(3))我们认为搜索树可以在对数步数中完成,但这是基于树是“平衡的”假设,即每棵树的左子树和右子树具有大约相同数量的元素,因此每个子树包含大约一半的父树元素。但是,我们怎么能确定我们建造的树将是平衡的呢?即使我们从平衡树开始,使用 adjoin_set 添加元素也可能产生不平衡的结果。因为新附加元素的位置取决于该元素与元素列表中已有元素的比较,因此我们可以预期,如果我们“随机”添加元素,树将倾向于“平衡”。
但这并不是一定的。例如,如果我们从一个空集合开始,并按顺序连接数字 1 到 7,我们最终会得到一个高度不平衡的树,其中所有左侧子树都是空的,因此它与简单有序列表相比没有任何优势。解决此问题的一种方法是定义一个操作,将任意树转换为具有相同元素的平衡树。我们可以在每隔几次 adjoin_set 操作之后执行此转换,以保持集合的平衡。
译者:可见 浙江大学慕课:平衡二叉树
交集和并集操作可以在线性时间内通过将树结构转换为有序列表和返回来执行。将留作练习。
Python 的集合实现方法:Python 内置的 set 类型不使用任何这些表示。相反,Python 使用一种表示法,该表示法基于一种称为哈希(hashing)的技术提供恒定时间的成员关系测试和相邻操作,这是另一门课程的主题。内置的 Python 集合不能包含可变数据类型,如列表、字典或其他集合。为了允许嵌套集,Python 还有一个内置的不可变 frozenset 类,它与 set 类共享方法,但不包括改变方法和操作符。