1.6 高阶函数

INFO

译者：mancuoj、clcs

来源：1.6 Higher-Order Functions

对应：Disc 01、Disc 02、HW 02、Lab 02、Hog

我们已经看到，函数作为一种抽象方法，描述了与具体参数值无关的复合操作。例如，在 square 函数中：

>>> def square(x):
        return x * x

我们谈论的并不是某个特定数字的平方，而是一种求任意数字平方的方法。

当然，我们完全可以不定义这个函数，而每次都直接写：

>>> 3 * 3
9
>>> 5 * 5
25

从来不显式提到 square。对于像求平方这样简单的计算，这种做法倒也够用；但如果遇到更复杂的例子，比如求绝对值 abs 或者斐波那契数 fib，再这么写就会变得非常繁琐。

一般来说，如果语言中缺少函数定义能力，我们就只能始终停留在语言所提供的那些基本操作（这里是乘法）的层面工作，而无法用更高层次的操作来思考问题。我们的程序虽然仍然能算出平方，但我们的语言本身却失去了表达“求平方”这个概念的能力。

一个强大的编程语言应该具备的能力之一，就是能够通过给常见模式命名来建立抽象，然后直接使用这些名字来编程。函数正是提供了这种能力。

正如我们在接下来的例子中所见，代码中经常会出现一些反复使用的编程模式，只是每次配合使用的具体函数不同。这些模式同样可以通过命名来进行抽象。

为了将特定的通用模板表达为具名的概念（named concepts），我们需要构造一种可以接收其他函数作为参数或可以把函数当作返回值的函数。这种可以操作函数的函数就叫做高阶函数（higher-order functions）。

本节将展示高阶函数如何作为一种强大的抽象机制，极大地增强语言的表达能力。

1.6.1 函数作为参数

思考以下三个计算求和的函数。

第一个函数 sum_naturals 会计算从 1 到 n 的自然数之和：

>>> def sum_naturals(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + k, k + 1
        return total

>>> sum_naturals(100)
5050

第二个函数 sum_cubes 函数会计算 1 到 n 的自然数的立方之和。

>>> def sum_cubes(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + k*k*k, k + 1
        return total

>>> sum_cubes(100)
25502500

第三个函数 pi_sum 会计算下列各项的总和，它的值会非常缓慢地收敛到 $\pi$ 。

$$\frac{8}{1\cdot 3}+\frac{8}{5\cdot 7}+\frac{8}{9\cdot 11}+\dots$$

>>> def pi_sum(n):
        total, k = 0, 1
        while k <= n:
            total, k = total + 8 / ((4*k-3) * (4*k-1)), k + 1
        return total

>>> pi_sum(100)
3.1365926848388144

这三个函数明显有着共同的底层模式。它们几乎完全一样，唯一的区别在于函数名，以及用来计算每一项的那个关于 k 的表达式。

我们其实可以通过填充同一个模板的槽位来生成这些函数：

def <name>(n):
    total, k = 0, 1
    while k <= n:
        total, k = total + <term>(k), k + 1
    return total

这种共同模式的存在，强烈暗示这里有一个有价值的抽象正等待被提炼出来。 这三个函数本质上都是“对某项进行求和”。作为程序设计者，我们希望我们的语言足够强大，能够直接写出一个表达“求和”这个概念本身的函数，而不是只能写出计算某些特定和的函数。

在 Python 中做到这一点其实很简单：把上面模板中的“槽位”变成形式参数即可。

在下面的示例中，summation 函数接收两个参数：上界 n 和一个计算第 k 项的函数 term。我们可以像使用任何函数一样使用 summation，它简洁地表达了求和的概念。

花点时间单步调试（step through）走完这个示例，注意函数如何将 cube 绑定到局部名称 term 上以确保 $1\times 1\times 1+2\times 2\times 2+3\times 3\times 3=36$ 被正确计算出来。

通过使用一个直接返回其参数的恒等函数 identity，我们也可以使用完全相同的 summation 函数对自然数求和。

>>> def summation(n, term):
        total, k = 0, 1
        while k <= n:
            total, k = total + term(k), k + 1
        return total
>>> def identity(x):
        return x
>>> def sum_naturals(n):
        return summation(n, identity)
>>> sum_naturals(10)
55

summation 也可以直接被调用，而无需为特定的序列去定义另一个函数。

>>> summation(10, square)
385

可以定义 pi_term 函数来计算每一项的值，从而利用 summation 的抽象来定义 pi_sum 函数。传入参数 1e6（1 * 10 ⁶ = 1000000 的简写）以计算 $\pi$ 的近似值。

>>> def pi_term(x):
        return 8 / ((4*x-3) * (4*x-1))
>>> def pi_sum(n):
        return summation(n, pi_term)
>>> pi_sum(1e6)
3.141592153589902

1.6.2 函数作为通用方法

我们最初引入用户自定义函数，是为了把数值运算的模式抽象出来，使其不再依赖于具体的数字。

而当我们引入高阶函数后，开始出现一种更强大的抽象形式：有些函数表达的是通用的计算方法，与它们具体调用的函数无关。

尽管函数的含义在概念上得到了这样的扩展，但我们用来求值调用表达式的环境模型依然适用，无需任何改变。

当一个用户定义的函数被应用到某些参数上时，形式参数会在一个新的局部帧中绑定到这些参数的值（即便这些值是函数也不例外）。

思考下面的例子，它实现了一种通用的迭代改进（iterative improvement）算法，并使用它来计算黄金分割率。黄金分割率 通常被称为“phi”，是一个接近 1.6 的数字，广泛出现在自然、艺术和建筑中。

迭代改进算法的原理是：从一个方程解的 guess（推测值）开始，重复应用 update 函数来改进该值，并调用 close 比较来检查当前的 guess 值是否已经足够接近正确值。

>>> def improve(update, close, guess=1):
        while not close(guess):
            guess = update(guess)
        return guess

这个 improve 函数是重复优化（repetitive refinement）这一过程的通用表达。它并不会指定要解决什么具体问题：所有细节都留给了作为参数传入的 update 和 close 函数。

黄金分割率有一个著名的特性：它可以通过反复把任意正数的倒数加 1 来逼近；同时它也满足“比它的平方小 1”这个关系。我们可以把这些性质表达成函数，供 improve 使用：

>>> def golden_update(guess):
        return 1/guess + 1

>>> def square_close_to_successor(guess):
        return approx_eq(guess * guess, guess + 1)

这里我们调用了 approx_eq 函数：如果其参数近似相等，则返回 True。我们可以通过比较两个数字差的绝对值是否小于一个微小的容差（tolerance value）来实现它：

>>> def approx_eq(x, y, tolerance=1e-15):
        return abs(x - y) < tolerance

以 golden_update 和 square_close_to_successor 为参数来调用 improve 将计算出黄金分割率的一个有限近似值。

>>> improve(golden_update, square_close_to_successor)
1.6180339887498951

通过追踪求值步骤，我们可以看到这个结果是如何计算出来的。首先，将 update、close 和 guess 绑定在 improve 创建的局部帧上。然后在 improve 的函数体中，将名称 close 绑定到 square_close_to_successor ，它会使用 guess 的初始值进行调用。跟踪其余步骤来查看其逐步演变为黄金分割率的计算过程。

这个例子说明了计算机科学中两个相关的重要思想：

1. 通过命名和函数，我们能够把大量复杂性抽象掉。虽然每个单独的函数定义都很简单，但由求值规则驱动起来的整个计算过程却相当精巧。
2. 正是因为 Python 拥有极其通用的求值过程，我们才能把这些小小的组件组合成复杂的计算。理解程序的解释过程（即求值规则），让我们能够验证和检查自己创造出来的计算过程。

一如既往，我们的新通用方法 improve 需要测试来检查其正确性。黄金分割比恰好有一个精确的闭合形式解，可以拿来做对比：

>>> from math import sqrt
>>> phi = 1/2 + sqrt(5)/2
>>> def improve_test():
        approx_phi = improve(golden_update, square_close_to_successor)
        assert approx_eq(phi, approx_phi), 'phi differs from its approximation'
>>> improve_test()

对于这个测试，没有消息就是好消息：improve_test 函数在 assert 语句执行成功后会返回 None。

1.6.3 定义函数 III：嵌套定义

上面的例子已经展示了：让函数作为参数传递的能力，极大地增强了我们编程语言的表达力。每一个通用概念或方程都可以对应一个短小的函数。

但这种做法也有两个负面后果：

1. 全局环境中塞满了各种小函数的名字（全局帧混乱），而且这些名字都必须全局唯一；
2. 我们还受到特定函数签名的限制：improve 的 update 参数只能接受一个参数。

嵌套函数定义（Nested function definition）可以同时解决这两个问题，但需要我们进一步丰富环境模型。

现在考虑一个新问题：求一个数的平方根（在编程语言中常简写为 sqrt）。反复应用下面的更新规则，可以收敛到 a 的平方根：

>>> def average(x, y):
        return (x + y)/2

>>> def sqrt_update(x, a):
        return average(x, a/x)

但这个需要两个参数的 sqrt_update 无法直接传给 improve（因为 improve 要求 update 只接受一个参数）。

更好的办法是把函数定义放在另一个函数的内部：

>>> def sqrt(a):
        def sqrt_update(x):
            return average(x, a/x)
        def sqrt_close(x):
            return approx_eq(x * x, a)
        return improve(sqrt_update, sqrt_close)

就像局部赋值一样，局部的 def 语句只影响局部帧。这些内部定义的函数只在 sqrt 被求值期间有效。按照我们的求值规则，这些内部的 def 语句甚至要等到 sqrt 被调用时才会真正执行。

词法作用域（Lexical scope）：局部定义的函数还能访问它们被定义时所在环境中的名字绑定。

在这个例子中，sqrt_update 引用了名字 a，而 a 是外层函数 sqrt 的形式参数。

这种在嵌套定义之间共享名称的规则称为词法作用域。关键在于：内部函数访问的是它被定义时的环境，而不是它被调用时的环境。

为了支持词法作用域，我们需要对环境模型做两点扩展：

1. 每一个用户定义的函数都有一个父环境：即它被定义时所在的环境。
2. 当调用一个用户定义的函数时，它创建的局部帧会扩展它的父环境。

在 sqrt 之前，所有函数都定义在全局环境中，所以它们的父环境都是全局环境。

而当 Python 执行 sqrt 函数体前两行时，它创建的 sqrt_update 和 sqrt_close 两个函数关联的都是 sqrt 的局部环境。

>>> sqrt(256)
16.0

在这次调用中，环境首先为 sqrt 创建一个局部帧，绑定 a = 256，然后执行其中的 def 语句，创建 sqrt_update 和 sqrt_close 两个函数对象。

这两个函数对象从此以后都带有父环境指针，指向 sqrt 的局部帧（我们标记为 f1）。

从现在开始，我们在环境图中会为每个函数值增加一个新的标注——parent（父环境）。

• 函数值的父环境即定义该函数时所在环境的第一帧。
• 如果一个函数没有标注 parent，则说明它定义在全局环境中。
• 当我们调用一个用户定义的函数时，新创建的帧会继承该函数的 parent 作为自己的父帧。

随后，名称 sqrt_update 这个名字被解析为刚刚定义的那个函数对象，并作为参数传给了 improve。在 improve 的函数体中，我们需要把 update（此时绑定为 sqrt_update）应用到初始猜测值（guess=1，也就是这里的 x=1）。这次应用会为 sqrt_update 创建了一个新的局部帧，这个帧里只有 x 的绑定，但它的父帧仍然是 sqrt 的帧（f1），而 f1 中仍然保留着 a = 256 的绑定。

求值过程中最关键的一点就是：sqrt_update 的 parent 被传递给了它被调用时所创建的新帧。新帧因此也被标注为 [parent=f1]。

级联环境（Extended Environments）：一个环境可以由任意长的帧链构成，并且总是以全局帧结束。

在 sqrt 这个例子之前，环境最多只包含两种帧：局部帧和全局帧。而通过使用嵌套的 def 语句定义函数并调用它们，我们可以创建更长的（帧）链。此次调用 sqrt_update 的环境由三个帧组成：

• sqrt_update 局部帧
• 它的父帧 f1（sqrt 的帧，包含 a = 256）
• 全局帧

在 sqrt_update 函数体的返回表达式 average(x, a/x) 中查找名字 a 时，会沿着这条环境链逐层查找：

• 先查当前帧（sqrt_update 的局部帧）→ 没有 a
• 再查父帧（f1，即 sqrt 的帧）→ 找到 a = 256
• 于是成功解析出 a 的值

这就实现了词法作用域的两个关键优势：

1. 局部函数的名字不会与外部（包括全局）名字冲突，因为它们被绑定在自己被定义的局部环境中，而不是全局环境。
2. 局部函数可以访问外层函数的环境，因为它的函数体是在定义时所在的环境的扩展环境中被求值的。

sqrt_update 这个函数携带了一些数据——即它定义时环境中引用的 a 的值。因为它们以这种方式“封装”信息，所以这种在局部定义的函数通常被称为闭包（closures）。

1.6.4 函数作为返回值

通过创建将函数作为返回值的函数，我们可以在我们的程序中实现更强大的表达能力。词法作用域编程语言的一个重要的特性是：局部定义的函数在被返回时，依然会保留它们的父环境。下面的例子展示了这一特性的实用价值。

一旦定义了许多简单的函数，函数复合（composition）就成为编程语言中的一种自然的组合方式。

也就是说，给定两个函数 f(x) 和 g(x)，我们可能想要定义 h(x) = f(g(x))。我们可以使用现有的工具来实现函数复合：

>>> def compose1(f, g):
        def h(x):
            return f(g(x))
        return h

此示例的环境图展示了如何正确解析名称 f 和 g，即使它们存在名称冲突。

compose1 中的 1 表示被复合的函数都只接受单个参数。这个命名惯例不是解释器强制要求的，只是函数名的一部分，用来提醒阅读代码的人。

至此，我们开始体会到精确定义“环境模型”所带来的好处。我们不需要对现有的环境模型做任何修改，就能完美解释这种返回函数的能力。

1.6.5 示例：牛顿法

这个扩展示例展示了函数返回值和局部定义如何协同工作，从而简洁地表达通用思想。我们将实现一种在机器学习、科学计算、硬件设计和优化领域广泛使用的算法。

牛顿法（Newton's method）是一种经典的迭代方法，用于寻找使某个数学函数返回 0 的参数值，这些值被称为函数的零点（zeros）。求函数的零点往往等价于解决某个我们真正感兴趣的问题，例如求平方根。

在继续之前先说一句感慨：我们很容易把“会求平方根”这件事当成理所当然。不只是 Python，你的手机、浏览器、计算器都能直接给你算出来。然而，学习计算机科学的一部分，就是要去理解这些量是如何被计算出来的。这里介绍的通用方法，适用于求解一大类 Python 内置之外的方程。

牛顿法本质上也是一种迭代改进算法：它对任何可微（differentiable）函数（即在任意点都可以用直线近似）的零点猜测进行改进。牛顿法通过追踪这些线性近似（linear approximations）来寻找零点。

试想一条穿过点 $(x,f(x))$ 的直线与函数 $f(x)$ 在该点拥有相同的斜率。这样的直线称为切线（tangent），它的斜率我们称为 $f$ 在 $x$ 处的导数（derivative）。

这条直线的斜率是函数值变化量与函数自变量的比值。所以，从当前 $x$ 沿着切线方向移动 $f(x)/\mathrm{斜}\mathrm{率}$ 的距离，就会得到切线到达 0 时的参数值。

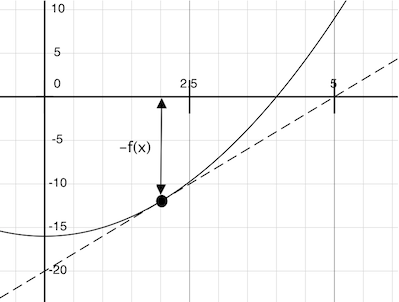
newton_update 表示函数 $f$ 及其导数 $\mathrm{d}f$ 沿着这条切线到 0 的计算过程。

>>> def newton_update(f, df):
        def update(x):
            return x - f(x) / df(x)
        return update

最后，我们可以使用 newton_update、improve 算法以及比较 $f(x)$ 是否接近 0 来定义 find_zero：

>>> def find_zero(f, df):
        def near_zero(x):
            return approx_eq(f(x), 0)
        return improve(newton_update(f, df), near_zero)

计算根：我们可以使用牛顿法来计算任意次方根，a 的 n 次方根就是使得 $x\cdot x\cdot x\cdots x=a$ 的重复 n 次的 $x$ 的值，例如：

• 64 的平方根是 8, 因为  $8\cdot 8=64$
• 64 的三次方根是 4, 因为  $4\cdot 4\cdot 4=64$
• 64 的六次方根是 2，因为 $2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2=64$

我们可以使用牛顿法根据以下观察结果来计算根：

• 64 的平方根 (写作 $\sqrt{64}$) 是使得  $x^2-64=0$ 的 $x$ 的值
• 推广来说，a 的 n 次方根 (写作 $\sqrt[n]{a}$) 是使得  $x^n-a=0$ 的 $x$ 的值

如果我们可以找到最后一个方程的零点，那么我们就可以计算出 n 次方根。通过绘制 n 等于 2、3 和 6，a 等于 64 的曲线，我们可以将这种关系可视化。

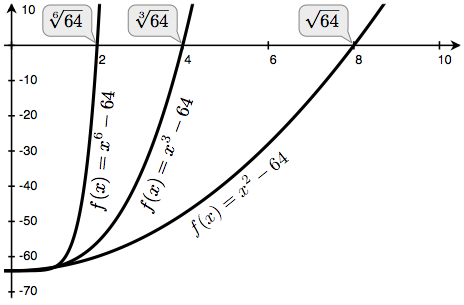
我们首先通过定义 $f$ 和它的导数 $\mathrm{d}f$ 来实现 square_root_newton 函数，根据微积分知识，$f(x)=x^2-a$ 的导数是线性方程 $\mathrm{d}f(x)=2x$。

>>> def square_root_newton(a):
        def f(x):
            return x * x - a
        def df(x):
            return 2 * x
        return find_zero(f, df)

>>> square_root_newton(64)
8.0

推广到 n 次方根，我们可以得到 $f(x)=x^n-a$ 和它的导数 $\mathrm{d}f(x)=n{x}^{n-1}$。

>>> def power(x, n):
        """返回 x * x * x * ... * x，n 个 x 相乘"""
        product, k = 1, 0
        while k < n:
            product, k = product * x, k + 1
        return product

>>> def nth_root_of_a(n, a):
        def f(x):
            return power(x, n) - a
        def df(x):
            return n * power(x, n-1)
        return find_zero(f, df)

>>> nth_root_of_a(2, 64)
8.0
>>> nth_root_of_a(3, 64)
4.0
>>> nth_root_of_a(6, 64)
2.0

所有这些计算中的近似误差都可以通过将 approx_eq 中的 tolerance 调小来进一步减小。

在使用牛顿法时要注意，它并非总是收敛。初始猜测必须足够接近零点，而且函数本身需要满足一些条件。尽管有这些局限，牛顿法仍然是求解可微方程的一种极其强大且通用的计算方法。现代计算机中对数运算和大整数除法的高效算法，就大量采用了牛顿法及其变种。

1.6.6 柯里化

我们可以用高阶函数把一个接受多个参数的函数，转换成一系列只接受单个参数的函数链。

具体来说，给定一个函数 f(x, y)，我们可以定义一个函数 g 使得 g(x)(y) 等价于 f(x, y)。这里 g 是一个高阶函数，它接受单个参数 x 并返回另一个接受单个参数 y 的函数。这种转换就称为柯里化（curring）。

例如，我们可以定义 pow 函数的柯里化版本：

>>> def curried_pow(x):
        def h(y):
            return pow(x, y)
        return h
>>> curried_pow(2)(3)
8

一些编程语言（如 Haskell）只允许单参数函数，因此程序员必须对所有多参数过程进行柯里化。在 Python 等更通用的语言中，当我们需要一个只接受单个参数的函数时，柯里化就很有用。

例如，map 模式就是把一个单参数函数应用到一系列值上。在下个章节中，我们将看到更通用的 map 模式的示例，现在我们可以先实现一个简单的 map_to_range：

>>> def map_to_range(start, end, f):
        while start < end:
            print(f(start))
            start = start + 1

我们可以使用 map_to_range 和 curried_pow 来打印 2 的前十次幂，而无需专门为 2 写一个幂函数：

>>> map_to_range(0, 10, curried_pow(2))
1
2
4
8
16
32
64
128
256
512

同样地，我们可以用这两个函数计算其他底数的幂。柯里化让我们无需为每个底数都写一个专用函数。

上面我们手动对 pow 进行了柯里化，得到了 curried_pow。其实我们可以定义通用的柯里化和反柯里化（uncurrying）函数：

>>> def curry2(f):
        """返回给定的双参数函数的柯里化版本"""
        def g(x):
            def h(y):
                return f(x, y)
            return h
        return g
>>> def uncurry2(g):
        """返回给定的柯里化函数的双参数版本"""
        def f(x, y):
            return g(x)(y)
        return f
>>> pow_curried = curry2(pow)
>>> pow_curried(2)(5)
32
>>> map_to_range(0, 10, pow_curried(2))
1
2
4
8
16
32
64
128
256
512

curry2 函数接受一个双参数函数 f 并返回一个单参数函数 g。当 g 应用于参数 x 时，它返回一个单参数函数 h。当 h 应用于参数 y 时，它调用 f(x, y)。因此，curry2(f)(x)(y) 等价于 f(x, y) 。uncurry2 函数反转了柯里化变换，因此 uncurry2(curry2(f)) 等价于 f。

>>> uncurry2(pow_curried)(2, 5)
32

1.6.7 Lambda 表达式

到目前为止，每次我们要定义新函数，都得给它起个名字。但对于其他类型的表达式，我们并不需要给中间值命名。

也就是说，我们可以计算 a * b + c * d 而不必命名子表达式 a*b 或 c*d 或完整的表达式。

在 Python 中，我们可以使用 lambda 表达式实时创建函数（匿名函数）。lambda 表达式求值后得到一个函数，这个函数的函数体只有一个返回表达式，不允许出现赋值或控制语句。

>>> def compose1(f, g):
        return lambda x: f(g(x))

可以用一句英文来理解 lambda 表达式的结构：

lambda              x         :              f(g(x))
"A function that    takes x   and returns    f(g(x))"

lambda 表达式的结果称为 lambda 函数。它本身没有名字（ Python 会显示 <lambda>），但其他行为和普通函数完全一样。

>>> s = lambda x: x * x
>>> s
<function <lambda> at 0xf3f490>
>>> s(12)
144

在环境图中，lambda 表达式的结果也是一个函数，用希腊字母 λ（lambda）来标注名字。用 lambda 可以把 compose1 写得非常紧凑：

有些程序员觉得用 lambda 创建的匿名函数更简洁直接。但复合的 lambda 表达式虽然短，却常常难以阅读。例如下面这行虽然正确，但很多人一眼看不懂：

>>> compose1 = lambda f,g: lambda x: f(g(x))

一般来说，Python 的风格指南更推荐使用显式的 def 语句，而不是 lambda。但在需要把简单函数作为参数或返回值时，lambda 是被允许且合适的。

这些风格规则只是指导意见，你完全可以按自己的喜好编程。但写代码时，不妨想想将来可能阅读你代码的人——当你让程序更容易理解时，你就是在帮他们的忙。

术语 lambda 其实是个历史意外，源于早期数学符号与排版技术的冲突。

It may seem perverse to use lambda to introduce a procedure/function.

The notation goes back to Alonzo Church, who in the 1930's started with a "hat" symbol, he wrote the square function as "ŷ . y × y".

But frustrated typographers moved the hat to the left of the parameter and changed it to a capital lambda: "Λ y . y × y";

From there the capital lambda was changed to lowercase, and now we see "λ y . y × y" in math books and (lambda (y) (* y y)) in Lisp.

— Peter Norvig (norvig.com/lispy2.html)

尽管词源有些奇特，lambda 表达式以及对应的函数应用形式语言——λ演算（lambda calculus）——都是计算机科学中最核心的概念之一，远远超出了 Python 社区的范畴。我们将在第 3 章研究解释器设计时再次回到这个话题。

1.6.8 抽象与一等函数

本节开头我们就指出，用户自定义函数是一种至关重要的抽象机制，因为它们让我们能把通用的计算方法作为编程语言中的显式元素表达出来。现在我们又看到，高阶函数允许我们操作这些通用方法，从而创造更进一步的抽象。

作为程序员，我们应该时刻留意程序中潜在的底层抽象，基于它们进行构建，并泛化出更强大的抽象。这并不是说永远要用最抽象的方式写程序——高手知道如何选择与任务相匹配的抽象层次。但重要的是，我们要能用这些抽象去思考，这样在新的场景中才能迅速应用它们。

高阶函数的意义在于，它们让我们能把这些抽象显式地表示为编程语言中的元素，像对待其他计算元素一样去操作它们。

一般来说，编程语言会对计算元素的操作方式施加各种限制。限制最少的元素被称为具有一等地位（first-class status）。一等元素通常享有以下“权利和特权”：

1. 可以绑定到名字
2. 可以作为参数传递给函数
3. 可以作为函数的结果返回
4. 可以出现在数据结构中

Python 授予函数完整的一等地位，由此带来的表达能力提升是巨大的。

1.6.9 函数装饰器

Python 提供了一种特殊语法，让我们在执行 def 语句时就能应用高阶函数，这种语法称为装饰器（decorator）。最常见的例子之一就是 trace：

>>> def trace(fn):
        def wrapped(x):
            print('-> ', fn, '(', x, ')')
            return fn(x)
        return wrapped

>>> @trace
    def triple(x):
        return 3 * x

>>> triple(12)
->  <function triple at 0x102a39848> ( 12 )
36

在这个例子中，高阶函数 trace 返回一个新函数，它会在调用原始函数前打印一行跟踪信息。

@trace 注解改变了 def 的执行规则：虽然还是先创建了 triple 函数，但名字 triple 最终绑定的并不是这个原始函数，而是 trace(triple) 的返回值。

等价的非装饰器写法是：

>>> def triple(x):
        return 3 * x
>>> triple = trace(triple)

在本书相关的项目中，装饰器常被用于跟踪函数调用，或者在命令行运行程序时选择要执行哪些函数。

专家扩展：@ 符号后面也可以跟一个调用表达式。@ 后面的表达式先被求值（就像上面的 trace），然后执行 def，最后把装饰器表达式的结果应用到新定义的函数上，并把最终结果绑定到 def 中的名字。